Lời giải bài toán siêu học búa chỉ 0,001% người làm đúng

Bài toán hóc búa của kỳ thi SAT năm 1982 được ra dưới dạng trắc nghiệm và chỉ có 3 trong số 300.000 người làm đúng.

Bài toán hóc búa chỉ 3 trong số 300.000 người làm đúng.

SAT là một kỳ thi phổ biến nhằm sát hạch học sinh, sinh viên trong các kỳ thi tuyển sinh vào hệ đại học, cao đẳng tại Mỹ. Kỳ thi này được tiến hành và giám sát bởi hiệp hội College Board (một hiệp hội của các trường học và cao đẳng tại Mỹ).

Phần thi SAT Reasoning Test (còn được biết đến là SAT- I) sẽ kiểm tra khả năng tư duy logic và phân tích vấn đề của các thí sinh với mức điểm từ 600 đến 2.400 điểm. Trong mức giới hạn điểm này thí sinh có số điểm từ 1.800 trở lên có nhiều cơ hội cạnh tranh hơn khi nộp vào các trường đại học danh tiếng và uy tín. Đối với những tường đại học trong top 50 của bảng xếp hạng thì các thí sinh cần có số điểm trên 2.000.

Năm 1982, kỳ thi này đã đưa ra một bài toán khiến nhiều người tranh cãi gay gắt. Theo đó, chỉ có 3/300.000 thí sinh tham dự kỳ thi SAT năm ấy đưa ra đáp án đúng. Con số này tương ứng với tỷ lệ 0,001%.

Nhiều năm trôi qua, bài toán này vẫn được đánh giá là siêu hóc búa, khiến nhiều người căng não mỗi khi nhắc lại. Theo đó, đề bài cụ thể như sau:

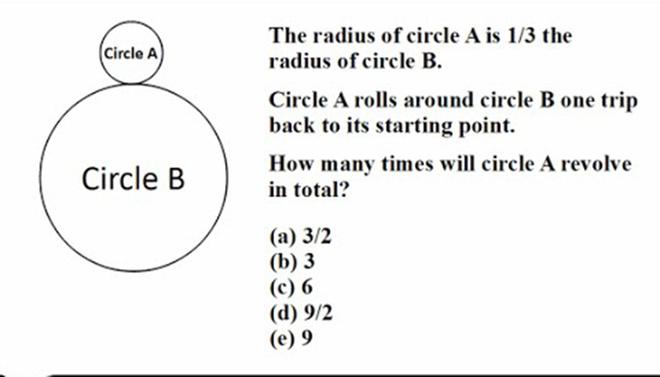
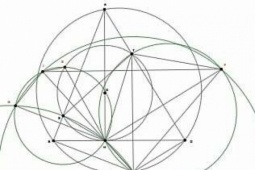
Bán kính hình tròn B gấp 3 lần bán kính hình tròn A. Nếu hình A lăn xung quanh hình B, nó phải thực hiện bao nhiêu vòng quay để trở lại điểm xuất phát?

=> Các phương án được đưa ra là 3/2, 3, 6, 9/2, 9 vòng.

Theo bài đăng ngày 25/5/1982 trên tờ Washington Post, cả 5 phương án trên đều sai.

Tác giả bài viết cho rằng câu hỏi nhắc đến "revolve" nghĩa là hình tròn A vừa tự xoay quanh nó vì xoay quanh hình tròn B. Vì vậy, đáp án thực sự của bài toán là 4 vòng (không trùng với những phương án đề đưa ra).

Nguồn: [Link nguồn]Nguồn: [Link nguồn]