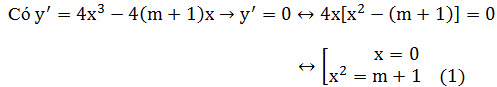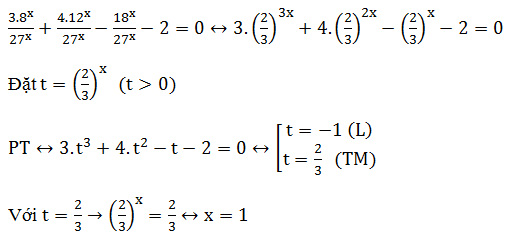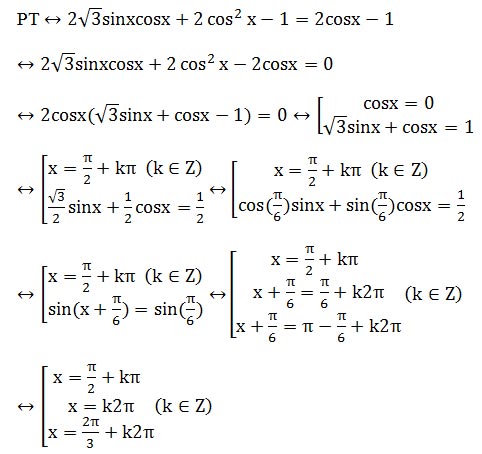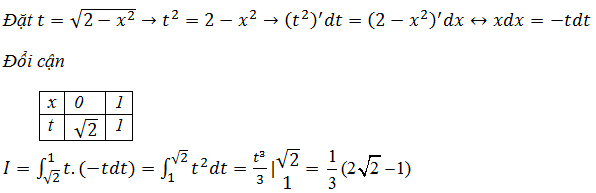Dạng bài tập dễ xuất hiện trong đề thi ĐH môn Toán

Trong đề thi đại học những năm gần đây, các dạng bài tập về hàm số, phương trình, bất phương trình, hệ phương trình số mũ Logarit… thường được đề cập tới.

Thầy Phạm Quốc Vượng, giáo viên luyện Toán ở Hà Nội chia sẻ về các dạng câu hỏi học sinh dễ bị đánh “lừa” trong khi làm bài thi đại học, cao đẳng môn Toán.

Thầy Vượng cho hay, theo dõi đề thi đại học những năm gần đây thấy rằng đề thi thường cấu tạo 2 phần, phần  đại số chiếm 7 điểm và hình học chiếm 3 điểm. Phần đại số bao gồm các nội dung chính sau: hàm số, phương trình, bất phương trình, hệ phương trình mũ Logarit, phương trình lượng giác, bất đẳng thức, bài toán Min, Max… Phần hình học bao gồm các nội dung: Hình học giải tích phẳng, hình học không gian, hình học giải tích trong không gian.

Dạng bài tập hàm số:

Nội dung này thường chiếm 2 điểm trong đề thi, câu hỏi dạng này gồm 2 ý . Ý thứ nhất là khảo sát và vẽ đồ thị hàm số, ý này mặc định trong đề thi và là ý dễ hầu hết các em đều làm được. Ý thứ hai gọi là câu hỏi phụ khảo sát hàm số. Để làm được ý này các em cần đọc kỹ câu hỏi  sau đó chia câu hỏi thành các ý hỏi nhỏ và giải quyết từng ý hỏi một, đúng đến đâu các em có điểm đến đó.

Ví dụ đề thi đại học khối A năm 2012 có hỏi: Cho hàm số

a) Khảo sát và vẽ đồ thị hàm số (1) với m=0.

b) Tìm m để đồ thị hàm số (1) có ba điểm cực trị  tạo thành ba đỉnh của một tam giác cân.

Với câu hỏi này thí sinh có thể chia làm 3 ý hỏi nhỏ: ý hỏi thứ nhất là tìm m để đồ thị hàm số có 3 điểm cực trị, ý hỏi thứ hai là tìm tọa độ 3 đỉnh của tam giác (nghĩa là tìm tọa độ 3 điểm cực trị), ý hỏi thứ ba là tìm điều kiện để tam giác đó vuông.

Với ý hỏi thứ nhất: nói đến cực trị là nói đến phuơng trình y'=0, để có 3 cực trị học sinh nên đi tìm điều kiện để phương trình y'=0 có 3 nghiệm phân biệt.

Để có 3 cực trị khi và chỉ khi phuơng trình y'=0 có 3 nghiệm phân biệt <-> PT(1) có hai nghiệm phân biệt khác 0 <-> m + 1 > 0 <-> m > -1

Với ý hỏi thứ hai: thí sinh tìm 3 nghiệm của phương trình y'=0 sau đó học sinh thay vào hàm số ban đầu suy ra tọa độ 3 điểm cực trị.

Dạng bài tập nội dung phương trình, bất phương trình, hệ phương trình mũ Logarit

Với nội dung trong bài phương trình, bất phương trình, hệ phương trình mũ Logarit, học sinh nếu học theo dạng bài tập thì số lượng dạng bài tập nhiều, khi vào làm bài thi các em rất khó để nhớ ra dạng bài tập. Do vậy, học sinh nên lưu ý và giải chung theo các bước sau: tìm điều kiện; biến đổi các biểu thức mũ về các biểu thức mũ có số mũ chung; biến đổi các biểu thức mũ về cùng cơ số; nếu không đưa được cùng cơ số thì chia cả hai vế cho một biểu thức mũ có cơ số lớn nhất hoặc nhỏ nhất.

Sau đó nhóm thành phương trình, bất phương trình tích hoặc đặt ẩn phụ hoặc sử dụng phương pháp hàm số hoặc áp dụng công thức nghiệm suy ra giá trị x.

Đơn cử đề thi cho giải phương trình

Với phuơng trình này thí sinh có thể phân tích tích như sau: Phuơng trình này không cần điều kiện, các biểu thức mũ đã cùng số mũ là x, các biểu thức mũ có rất nhiều cơ số khác nhau 8,12, 18, 27 không đưa về cùng một cơ số được do đó học sinh nghĩ đến việc chia cả hai vế cho biểu thức 8^x hoặc 27^x và có lời giải cụ thể là:

Chia cả hai vế cho 27^x ta được:

Nội dung trong bài tập phương trình lượng giác

Để ôn thi tốt nội dung này ngoài việc lắm chắc các phuơng trình cơ bản các em học sinh cần lắm chắc kĩ năng biến đổi chung một phuơng trình lượng giác như nhau: tìm điều kiện; biến đổi các biểu thức lượng giác trong phương trình về cùng số đo góc. Nếu có nhiều số đo góc khác nhau không đưa được về chung số đo góc thì các em sử dụng công thức hạ bậc, biến tổng thành tích, biến tích thành tổng để chuyển thành phương trình tích  hoặc phuơng trình cơ bản để giải.

Chuyển các biểu thức lượng giác về cùng 1 hàm sau đó đặt ẩn phụ hoặc nhóm thành phuơng trình tích hoặc áp dụng các phương trình cơ bản để giải. Sau đó, kết hợp điều kiện.

Ví dụ đề thi đại học cho giải phương trình sau:

Với phương trình này học sinh phân tích như sau: Phương trình này không cần điều kiện, trong phương trình có 2 số đo góc là x và 2x vì thế học sinh nghĩ đến việc sử dụng công thức nhân đôi đưa về cùng số đo góc là x, sin2x chỉ có 1 công thức là sin2x=2sinx.cosx. Thế nhưng cos2x có tới 3 công thứcvấn đề đặt ra là sử dụng công thức nào. Nếu học sinh quan sát thay sin2x=2sinx.cosx  thì các biểu thức lượng giác còn lại trong phương trình đều chứa cosx, do đó lời giải sẽ như sau:

Nội dung trong nguyên hàm, tích phân và ứng dụng:

Ngoài việc lắm chắc công thức các em cần chú ý có 2 phương pháp chính thường xuyên sử dụng là phương pháp từng phần và phương pháp đổi biến số. Phương pháp từng phần thường được sử dụng với bài toán tính nguyên hàm và tích phân mà hàm dưới dấu nguyên hàm tích phân là tích của hai hàm số hoặc hàm dưới dấu nguyên hàm tích phân là hàm lnu, lnⁿ u.

Phương pháp đổi biến số: với tích phân hữu tỷ trước tiên học sinh tách hàm dươi dấu nguyên hàm tích phân thành các biểu  thức hữu tỷ đơn giản sau đó dùng phương pháp đổi biến số để tính. Còn với nguyên hàm tích phân mũ logarit ngoài các dạng từng phần còn lại các em sử dụng phương pháp đổi biến số để làm mất mũ logarit rồi tính.

Ví dụ: Đề thi đại học năm 2013 cho tính tích phân

Đây là tích phân hàm căn nên học sinh nghĩ đến đặt cả biểu thức căn bằng t trước chứ không nghĩ đên việc đặt lượng giác

mặc dù biểu thức căn có dấu hiệu đặt lượng giác, do vậy lời giải cụ thể sau:

Nội dung trong bài hình học:

Phần hình học không gian thường gồm 2 ý. Ý thứ nhất là tính thể tích, ý thứ hai là câu hỏi phụ đi kèm bao gồm các câu hỏi chứng minh vuông góc, tính góc, tính khoảng cách...với ý hỏi phụ này ngoài việc tính trực tiếp các em có thể sử dụng phương pháp giải tích để giải (dựng hệ trục tọa độ, tìm tọa độ các đỉnh sau đó sử dụng phương giải tích để tính toán).

Phần hình học giải tích phẳng và hình giải tích không gian các em cần chỉ ra các dạng toán chung và phương pháp giải chung đúng trong cả hình giải tích phẳng lẫn giải tích trong không gian.

Ví dụ bài toán tìm tọa độ điểm trong hình học giải tích phẳng và hình học giải tích trong không gian đều chung cách giải sau: Nếu điểm cần tìm thuộc đường thẳng cho trước thì ta chuyển đường thẳng về tham số , sau đó suy ra tọa độ điểm cần tìm theo t. Lập phương trình theo t, giải tìm t suy ra điểm cần tìm. Nếu điểm cần tìm không thuộc đường thẳng thì gọi điểm cần tìm là (x₀,y₀) hoặc (x₀,y₀,z₀).  Lập hệ phương trình rồi giải tìm nghiệm.