Đố vui: Bài toán hình vuông

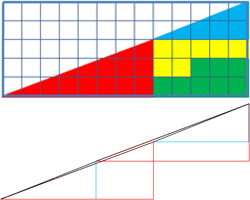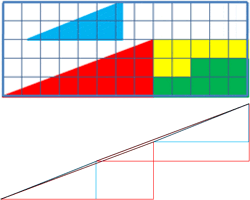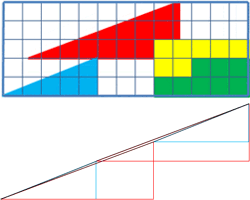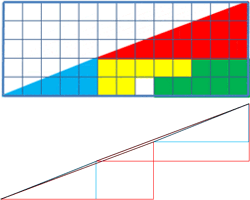
Cùng được ghép bằng 4 hình giống nhau, nhưng diện tích của tam giác khác nhau?

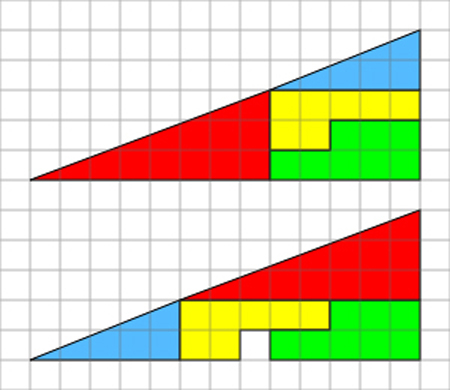
Bạn hãy nhìn hai tam giác trong hình vẽ, nếu lấy cạnh của một hình vuông nhỏ là 1 đơn vị, thì hai tam giác này đều có một cạnh bằng 5 và một cạnh bằng 13.

Mỗi tam giác lại chứa 4 hình (được tô thành 4 màu) giống hệt nhau, chỉ khác vị trí đặt. Tại sao tam giác thứ hai lại “hổng” một ô vuông, như vậy có nghĩa là dù được tạo bằng 4 hình như nhau nhưng diện tích tam giác thứ hai lại kém tam giác thứ nhất đúng bằng một ô vuông?
Sự vô lý nằm ở đâu?

>>> Trả lời: Đây là bài toán hình vuông nổi tiếng được cho là Paul Curry, một nhà ảo thuật nghiệp dư ở thành phố New York, nghĩ ra năm 1953.

Thực ra đây chỉ là vấn đề ảo giác. Nếu dùng thước kẻ thẳng để đo, bạn có thể nhận ra “cạnh huyền” của tam giác thứ nhất võng xuống, và “cạnh huyền” của tam giác thứ hai phồng lên chứ không phải là một đường thẳng.
Ô vuông “dư ra” chính bằng diện tích của hai đoạn “hơi cong cong” này ghép lại!

*
* *

Đố vui “tàng hình”: Cái gì luôn ở phía trước bạn, mà bạn không bao giờ nhìn thấy?

>>> Trả lời